Using chips

R-2

Which one works and why? \
Student A:

2x+4+6x-5+7x+3=17x

-No add-ons or coins
-Just add numbers then x at the end



Student B:

2x+4+6x-5+7x+3=15x+2

-Added together. 2x+6x=7x=15x



**If x= 1, then both would be right. 

Questions:
If problems are the same, why 2 answers?
Where is the +2 from?


Rule:
Never assume x=
Don't mix apples and oranges (strips and the chips, bags and the coins, x and add-ons)
Always show the add-on Don't mix the constant or an add-on 

Generalyzing linear equations and Quiz

x (indep. variable) * constant + sometimes an add on= y (depend. variable)

y=mx+b

m=constant
b=add on
y=dependent variable
x=independent variable


When you see two letters  or a number and a letter next to each other, it means they are multiplied.


Representations:
1. Graph
2. Table
3. Equation

Can you show where the...
1. constant of probortinality
2. add-on
...is in a graph, table, and equation

Can you create some representations related to a word problem

TMWYK: About the intersecting y-axis

-related to the add on
-indep. variable (x) goes from + to -
-if it hits the y-axis at 0 - no add on
-where the first point is


** Add on is the y-intercept. It starts someplace other than zero on the y-axis.

The add on in a linear equation and t-shirt problem

TMWYK:
-Extra part
-Add or subtract
-Happens w/ head start/up front price
-When linear graphs don't start at the same place

***Where it hits or intersects the y-axis (ex. 45 in headstart) it starts at 0. Add on is 0.


Walkathon T-shirt problem

Given these equations, what do you think the C and n could stand for? Could you make up a problem? 

Mighty T

C= 49 + n
C=cost
n=# of students 
49 to create a design (add on)


No-Shrink T

C=4.5n
C=cost
n=number of students 
No add on, hits 0 axis


R/L 63
Here is the dilemma. I have $120. Which place should I go to buy the maximum amount of t-shirts. 

-Need two ways to justify your thinking

Positive and negative constant of proportionality

 

Observations

-Goes down by 12 each time

-spend $12 each week

-money to time 

-Linear- consistent amount

 Rules

144- n x 12 = amount of $

-n x 12 + 144 = amount of $

12^2- n x 12

Graph

Starts at the top of the y-axis and goes down 

y is bigger than x

Positive and Negative Constant of Proportionality

      +                                                          -

n x constant                                  data pts go down

graph increases                            start at top of y-axis

indep and depen go up                -n x constant

                                                     week goes up (ind), $ goes down (dep)

L-55 Characteristics

Characteristics of a Linear:

Graph                                     Table                                        Equation
                                                                               *rule/equation can't change
                                                                               *find one of the axis in the equation
                                                                               *can create a graph from an equation
                                                                               *n x constant (what it goes up every time)
                                                                               *Goes up by each time (unit rate, constant of Prop)

Walkathon Plans

Walkathon

Plan A
$10 regardless of miles

Plan B
$2/ mile walked

Plan C
$5 regardless of miles plus $.50/ mile walked

Which plan would you make the most money for the least amount of miles?

Linear Graphs and Equations

TMWYK: Linear Graphs and equations

*equation helps find coordinates
*graphs-show data
*equations-help find data
*graph can help find rules
*Graph looks different
*Maybe it's a graph where coordinates make up a straight line

Coordinate Graphs

Core Math Goal: How can you determine if a relationship is linear or not?? How can you see this linear relationship in a model, table, graph, and equation?

TMWYK: Coordinate Graphs

*Neg and pos
*plot points to represent data
*x-axis shows a value
*x axis is independent variable, y axis the dependent variable
*Look for patterns

Patterns

TMWYK: How can you make rules from patterns
-observations
-predict
-see what it goes up by
-more/different rules
-Must work for everything
-Identify what each part of the equation does
-compare all scenarios



Pattern Rules-

1. (n*3)+1  n=figure #

2. Dark is negative, Grey is positive

(n*3)-1  n=figure #
(the minus 1 is from the middle square)

3. Dark is negative, grey is positive

(n*2)-((n*2)+4)  n=figure

**Class discovered that every figure is equal to -4.
Different Equation: 0-4   (The n*2-n*2 cancels out or zeroates)

4.0=-1   0=odd
   E=0    E=even

5.

6.

Chimp Problem

2 different ways to write ratio

part to part
part to whole

Fiber
2/5

Protein
3/5

Baby Chimps Part to Part ratios
2amounts fiber
3 amounts protein

40 amounts fiber
60 amounts protein

4 amounts fiber
6 amounts protein

3 amounts protein
2 amounts finber          (This one was flipped around 

R-41 Proportions

R-41 Core Math Goal: How can you use proportions to find percentages of a value when you know a certain percentage of the same value??


TMWYK: About creating a proportion

-set it up as a fraction (2 equivalent fractions)
-use scale factor
-two=fractions w/change between them (discount or raise in price)

100 =  200
123      X

R-41

Core Math Goal: How can you use the same proportions to find percentages of a value when you know a certain percentage of the same value?

TMWYK: About using proportions to solve problems


$22,500

Markup 10%

Original price=??

Strategy:

Delany's Idea

10+100=110 (full price + mark up price)

10         2050
110  =   22550 (price of the car)   

***Flynn's Idea: Maybe they need to be equivalent fractions. We   can check it with that. Scale factor is 205. This means that they are equal fractions and are in proportion.
Proportional Strategy

*We should divide by 11. 10 is the mark up price 
110
10   =   11

10% of 110=11



New Problem: 

22,770=resale price
Original proce=19,800

What is the markup?

Miles Driven and Gallons used

 

Rules/equation

gallons x 30=miles

miles/30=gallons 

Gallons of gas           Distance 

 1                                   30

 2                                   60

 3                                   90

Unit rate

1 gallon to 30 miles

1 mile to .03 gallons

R-24

What is the relationship between two similar figures? (Reptiles)

Scale Factor- Number I multiply side length or perimeter by to get similar figure

Side Length- in proportion smaller side length x scale factor= bigger side length

Perimeter- small perimeter x scale factor= bigger perimeter

Area- bigger shape side lengths are a multiple of smaller shape side lengths



If my original area is 3 and my scale factor is 2 (twice as big), how can I figure out what that new area is?



If my original area is 6 and I have a scale factor of 3(3 times as big), how can I figure 

 Rule: original area x (scale factor)^2 = bigger area

(scale factor)^2= scale factor x scale factor 

Reptiles

Reptiles

SHAPES THAT TESSALATE TO FORM SIMILAR SHAPES 

Mug Wumps and HW

Observations:
-Glug (x,3y) and Lug(3x,y) have the same area size
-Glug is as tall as bug
-Lug and Bug have the same width (x's are the same)
-Mug, Zug, and Bug are related because they are similar. Even x's and even y's.
-Lug and glug are imposters
-Lug is as tall as Mug (Their y's are the same)
-If x and y are multiplied by different numbers they will be imposters.

How to make an Imposter: 
**-Multiplied y more than x so it is taller.
**-Multiply x more than y so that it is wider.

How to make a Wump Family:
**-Multiply x and y by the same number

 

HOMEWORK!

L15 pg. 41 # 14 and #15 

What are some predictions we can make for a rule to move the Mug Wumps around on the graph? 

-subtract same # from x,y

-change y and x by the same #

-Multiply x and y by the same number. 

-Move to the side, change the x's. 

-change coordinates

-If you want to move it up maybe adding 

-to move sideways, you add to the x axis. to move up, you add to the y. 

R-17 Similar Figures

What characteristics would 2 shapes need in order to be similar?

 Class Ideas:
-Same shape, but smaller or bigger or rotated.
-Shapes w/ corresponding sides/ angles 
-Same angle measures but proportional side lengths
-Size increases or decreases



l-17 How are these similar figures?

Shapes
Angles
Sides/side lengths

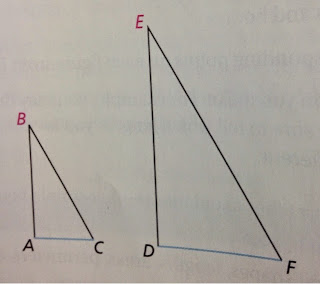
Corresponding sides and angles

 

Corresponding Sides: 

BA and ED

BC and EF

AC and DF

Corresponding Angles: 

B and E

A and D

C and F

 

Corresponding Sides:

HG and LK

GI and KJ

HI and LJ

Corresponding Angles:

H and L

G and K

I and J 

Homework: pg 20 # 18 and 19 

What is the definition for corresponding sides and angles? 

Corresponding angles- same angles

Corresponding stuff- proportion and same shape

 

PEMDAS- Order of Operations

It tells us the order to solve an equation

R-15

1.

-7 x 4 +8 ÷2

Division

How would you model
12 ÷4=3







Is it possible for the quotient for be anywhere else?  No, it's a fact family so it can switch around. 


L-11

What do you think you would write for a rule when dividing quotients?  Why? 

(+)÷(-)=(-)

(+)÷(+)=(+) No flips to red chips

(-)÷(-)=(-) Single flip. Middle is red. one side black. Other side red.

(-)÷(-)= (+)

÷